Формальна постановка задачі
TL;DR Як написати наукову статтю
Ця стаття показує структуру наукового дослідження, як процесу універсального (застововуваного до будь-якої області знань) вивчення феноменів за допомогою наукових методів. Ця структура однакова як для маленьких досліджень (як статті) так і для великих досліджень, що потребують формату монографії для свого висвітлення.
Синім кольором [тут] показані авторські коментарі для написання якісного формального дослідження, та його головної першої частини — "Формальна постановка задачі". В основу цього шаблону покладені стандарти на наукові дослідження інституту формальної математики "Групоїд Інфініті".
Вступ
У параграфі "Вступ" показується предмет та область дослідження та історична довідка про розвиток певного напрямку дослідження, його основні темоутворюючі статті та монографії. Також у вступі показується вид дослідження: фундаментальне це дослідження для побудови нових теорій чи прикладне дослідження для забезпечення виробничих чи наукових потреб.
Основоположниками верифікованої математичної логіки, основ математики, формальної математики та формальних методів можна вважати Бертрана Рассела та Альфреда Нотра Вайтхеда з їхньою роботою Principia Mathematica.
Зараз формальні методи верифікації та відповідно теорії на яких вони побудовані є актуальними засобами забезпечення математичної якості та гарантій для розробки не тільки програмного забезпечення, але і математики та навіть формальної філософії.
Актуальність
У параграфі "Акатуальність" показується як ці дослідження вже використовуються або можуть бути використані для забезпечення певних оптимізаційних показників. Актуальність показує глобальну мотивацію та важливість напрямку дослдідження. Контекст цієї частини більше розкривається в першій главі дослідження "Огляд існуючих рішень".
Ціна помилок в індустрії програмного забезпечення надзвичайно велика. Основні відомі приклади в індустрії: 1) Mars Climate Orbiter (1998), помилка невідповідності типів британської метричної системи, коштувала 80 мільйонів фунтів стерлінгів. Невдача стала причиною переходу NASA повністю на метричну систему в 2007 році. 2) Ariane Rocket (1996), причина4 катастрофи – округлення 64-бітного дійсного числа до 16-бітного. Втрачені кошти на побудову ракети та запуск 500 мільйонів доларів. 3) Помилка в FPU в перших Pentium (1994), збитки на 300 мільйонів доларів. 4) Помилка в SSL (heartbleed), оцінені збитки у розмірі 400 мільйонів доларів. 5) Помилка у логіці бізнес-контрактів EVM (неконтрольована рекурсія), збитки 50 мільйонів, що привело до появи верифікаторів та валідаторів контрактів. Більше того, і найголовніше, помилки у програмному забезпеченні можуть коштувати життя людей.
Ціна помилок в математичних доведеннях теж актуальна та дотична до теми цієї роботи — формальної верифікації. Особливо великі доведення які складаються з багатьох сотень сторінок вимагають ретельної та кропіткої роботи рецензентів, що може бути замінено формальними доведеннями на мовах для доведення теорем.
Наукова новизна
Пагаграф "Наукова новизна" показує переводі та сучасні методи які природнім чином продовжує ця робота та привносить крапельку свого здобутку.
Починаючи з перших пруверів 60-х років таких як AUTOMATH, пізніших систем Жирара System F та сучасні фібраційні системи з залежними типами мови програмування та системи типів пройшли значний шлях. Сучасні теорії типів присвячені формалізації вищої математики, гомотопічної теорії, симпліціальної геометрії. А системи програмування абсорбували теорії паральних процесів Мілнера та формалізацію лінійних типів які маються застосування також до квантових обчислень та формалізації теоретичної фізики.
Дана робота ґрунтується на гомотопічній теорії типів для потреб математичних мовних засобів, а всі проміжні системи типів, такі як системи Жирара — для виробництва. Також ця робота розказує про сучасні середовища виконання, які здатні працювати без операційних систем та реазізуються свої систем розподілу часу (планувальники).
Інновація роботи полягає в побудові унікальної замкненої системи яка складається з: 1) системного програмного забезпечення – модального середовища виконання разом з інтерпретатором написаним на формальній мові, разом з базовою бібліотекою та архітектурою прикладного програмування N2O.TECH; 2) прикладного програмного забезпечення — системи вищих формальних мов, для яких надано моделі, імплементації та базова бібліотека разом з математичними компонентами.
Таким чином "Вступ", "Актуальність" та "Наукова новизна" показують місцезнаходження дослідження у великому просторі існуючих досліджень.
Після 5 років цього дослідження, виконавши у вигляді вправ декілька імплементацій мов, було прийнято рішення формально оформити всю роботу згідно академічних нормативів. Тому в цій секції дається формальна постановка задачі, яка складається з опису об’єкту та предмету дослідження, мети, цілей та завдань. Дається головна мотивація та аналіз результатів
Мотивація
Параграф "Мотивація" або основна ідея, яка спонукала автора до дослідження та розкриває основну думку твору, з якої починається шлях дослідження.
Одна з причин низького рівня впровадження у виробництво систем верифікації – це висока складність таких систем. Складні системи верифікуються складно. Ми хочемо запропонувати спрощений підхід до верифікації — оснований на поєднанні концепції компактних простих мовних ядер для створення специфікацій, моделей, перевірки моделей, доведення теорем у теорії типів з кванторами та концепції середовища виконання яке виконується на верифікованому інтерпретаторі певної апаратної архітектури.
Кожен інститут чи компанія інвестує в одну певну мову, для зосередження зусиль на одному проекті. Особливість цієї роботи полягає в побудові уніфікованої системи, яка комплексно підходить до вирішення проблеми розширення мовних ядер, та їх обчислювачів. Ця робота пропонує замкнений фреймворк, який складається з мінімальної системи мов, що покриваються максимальну кількість мовних синтаксисів та семантик. Крім того, попередні дослідники зосереджувались на побудові системних бібліотек для певного середовиша виконання та асоційованих з ним вищих мов (з відповідними біндінгами). На відміну від фокусних досліджень, ця робота пропонує мультидисциплінарний або мовний підхід, де ми зосереджуємося на побудові моделі, яка буде вбудовуватися з мінімальними зусиллями в основні аглебраїчні мови. У таблиці яка показує можливий ландшафт атаки мовних систем які можна вважати аналогічними підходами до побудови не тільки замкненого життєвого циклу мовного забезпечення, але і системи віртуалізації.
Мета
Мета показує результат глибоких роздумів про область та об'єкт дослідження, огляд існуючих рішень, певний трек апробації та досвід використання більшості рішень. Вона розкриває ідею щодо стоврення нового продукту і нового дослідження беручи до уваги попередні дослідження які формують науковий спадок теми дослідження. Мета фокусується на предметі дослідження і полягає в його розкритті.
Мета цього досдідження дослідити, побудувати концептуальну модель та реалізувати формальну систему мов, яка поглинає усі існуючі мови програмування та пропонує уніфікований фреймворк для математичного мовного запезпечення чистого (доведення теорем) та прикладного математика (спеціалізовані мови та чисельні обичслення).
Більш розширено: метою цього дослідження є побудова єдиної системи, яка поєднує формальне середовище виконання та систему верифікації програмного забезпечення з великим спектром мовних засобів, які допомагають вбудувати в себе максимальну кількість існуючих мов. Це прикладне дослідження, яке є сплавом фундаментальної математики та інженерних систем з формальними методами верицікації.
Завдання
Після сформованої ідеї дослідження будується стратегічний план робіт або завдання дослідження за допомогою якого реалізується мета дослідження.
Завданням цього дослідження є імплементація (апробація) специфікації системи мов на різних мовах програмування та типових системах. Для цього детально проводився аналіз усіх існуючих мов програмування (близько 2000), які детально прокатегоризовані в Енциклопедії Мов Програмування.
Цілі
Це глобальне завдання висого рівня деталізується на локальні цілі досліжнення які реалізуються в процесі роботи та часто виливаються в продукти дослідження.
Таким чином "Мотивація", "Мета", "Завдання" та "Цілі" розкривають та протоколюють активність дослідження від його мотиваційної ідеї до детальних цілей, що управляються стандартними засобами планування.
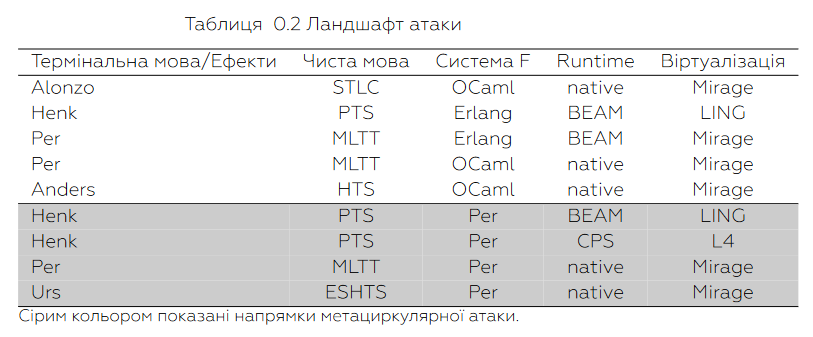
Головними цілями цього дослідження є побудова мінімальної системи мовних засобів для побудови ефективного циклу верифікації програмного забезпечення та доведення теорем. Основні компоненти системи, як продукт дослідження: 1) інтерпретатор безтипового лямбда числення; 2) компактне ядро — система з однією аксіомою; 3) мова з індуктивними типами; 4) мова з гомотопічним інтервалом [0, 1]; 5) уніфікована базова бібліотека середовища виконання; 6) бібліотека математичних компонент.
Об'єкт
Об'єкт дослідження, в залежност від спектру та розміру фокусу дослідження — це область знань, або її тема, або певна теорія, або певний об'єкт теорії з його властивостями.
Об'єкт дослідження — мови, системи програмування та системи доведення теорем, їх структурні моделі, архітектури та імплементації.
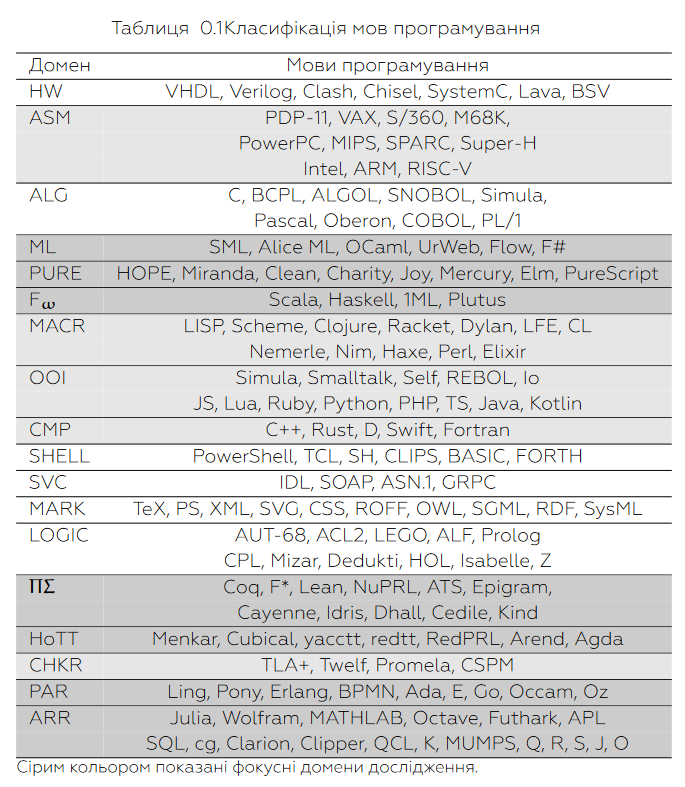
Більшо розширено: об'єктом дослідження данної роботи є: 1) системи верифікації програмного забезпечення; 2) системи доведення теорем; 3) мови програмування; 4) операційні системи, які виконують обчислення в реальному часі; 5) компактні середовища виконання.
Предмет
Предмет дослідження — це характеристики об'єкту дослідження, конкретна частина об'єкту дослідження, його універсальні властивості. Мета дослідження розкрити його предмет. Предмет розкриває сутність і показує властивості об'єкту дослідження.
Предмет дослідження у широкому сенсі — формальні моделі функціональних мов програмування з формальною семантикою. Предмет дослідження у вузькому сенсі — формальні системи Жирара, лямбда куб Барендрехта та гомотопічні системи, їх категорні моделі, що містять вичерпні математичні властивості.

Семантику мов, або властивості мовних категорій, що є предметом дослідження вивчає предмет теорія типів. Предметом та методом дослідження такої системи мов є теорія типів, як сучасний фундамент математики, який стисло та компактно представляє обчислювальне ядро не тільки теорії множин, але і теорії категорій, алгебраїчної топології та дифференціальної геометрії.
Теорія типів вивчає обчислювальні властивості мов та виділилася в окрему науку Пером Мартіном-Льофом як запит на вакантне місце у трикутнику теорій, які відповідають ізоморфізму Каррі-Говарда-Ламбека (Логіки, Мови, Категорії).
Таким чином, параграф "Об'єкт" розкриває формальну математичну модель об'єкту вивчення, а параграф "Предмет" розкриває предметні формальні математичні властивості об'єкту вивчення.
Методи
Загалом методи дослідження розділяються на теоретичні, проміжні та емпіричні. Теоретичні методи можуть включати розробку теорій, розв'язування рівнянь в цих теоріях використовуючи існуючі математичні засоби. Емпіричні методи пов'язані з замірами з використанням технологічних засобів, з самими обчисленнями. Проміжні методи застовуються як зворотній зв'язок який під впливом емпіричних результатів спостережень може вплинути на зміну теретичних методів та моделей.

Існує багадо підходів для формальної специфікації, верифікації та валідації, усі вони даються у розділі 1, де обгрунтувується вибір методу моделювання з використанням мови з залежними типами (теорії типів Мартіна-Льофа). Для разкриття семантки цього підходу використовується категорний метод та категоріальна логіка – теорія топосів. Теорія категорій довела свою корисність не тільки для математики, але і для програмного забезпечення.
Засоби
Засоби які були використанні при дослідженні: математичні, мовні, інформаційні, технологічні, тощо. До математичних засобів включаються математичні теорії, до мовних мови програмування, то інформаціних додаткове програме забезпечення, до технологічних апаратне забезпечення.
Таким чином, "Методи" та "Засоби" показують яким чином реалізується активність дослідження, його технічну математичну модель та частину, мову на якій слід читати результати дослідження.
Мови програмування розділені на чотири рівня як для клієнтської (мобільної та веб розробки) так і для серверної розробки (бекенд системи). Нульовий рівень — тотальні формальні алгебраїчні мови програмування, що забезбечують повноту, функціональність та доведення властивостей прогрм згідно сучасних уявлень про математичне моделювання та системи залежних типів побудованих на розшаруваннях. Перший рівень — формальні функціональні мови програмування, як правило System F, System F# які успішно використовуються в промисловості та забезпечують достатньо формальний запис який піддається масштабуванню у великих командах завдяки потужному ядру компіляторів. Другий рівень — неформальні (без формальної операційної чи денотаційної семантики) чи формальних верифікаторів, які проте успішно використовуються в промисловості, можуть бути як з розвиненими системами типів з узагальненими шаблонами та типами сумами, так і однотипними мовами програмування з динамічною типізацією. Третій рівень — мови які погано піддаються масштабуванню у промисловому виробництві (на основі спостережень за власним досвідом).
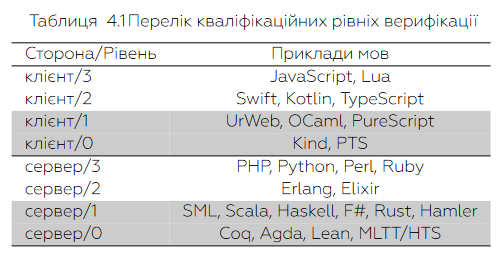
Практичні результати
Як правило добре дослідження окрім розкриття предмета дослідження залишає після себе побічні продукти дослідження, які виносять в "Практичні результати" дослідження. Часто проміжні цілі завдання дослідження стають вагомими та успішними продуктами.
Не зважаючи на нетривіальну структуру результатів, головним продуктом цього дослідження слід вважати загальний підхід описаний в цій роботій, який можна звести до наступних рекомендацій: 1) побудувати лінивий інтерпретатор CPS нетипизованого лямбда числення разом з системою процесів та чергами повідомлень на формальній мові; 2) побудувати мову числення конструкцій PTS на формальній мові з екстрактом у лінийвий інтерпретатор; 3) побудувати мову системи F Жирара або STLС для розробки базової бібліотеки для лінивого інтерпретатора; 4) побудувати базову бібліотеку для лінивого інтерпретатора; 5) побудувати індуктивну мову програмування MLTT; 6) побудувати гомотопічну мову програмування HoTT; 7) побудувати базову бібліотеку для гомотопічної мови; 8) побудувати бібліотеку теорем формальної математики.
Продукти дослідження
🌐 М.Сохацький. Формалізація математики.
🌐 М.Сохацький. Енциклопедія мов програмування.
🌐 М.Сохацький. Інститут формальної математики.
🌐 М.Сохацький. Одноаксіоматична система верифікації «Хенк».
🌐 М.Сохацький. Модальна гомотопічна мова математики «Андерс».
🌐 М.Сохацький. Кубічна бібліотека CCHM.